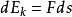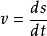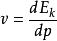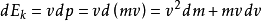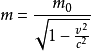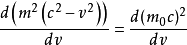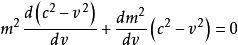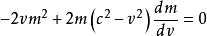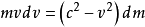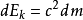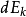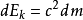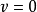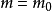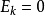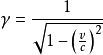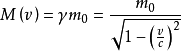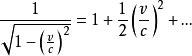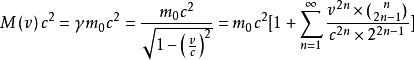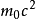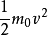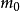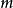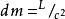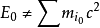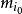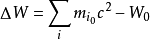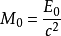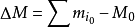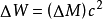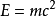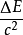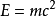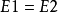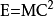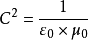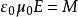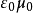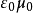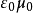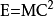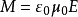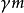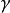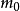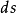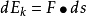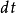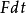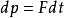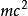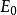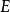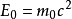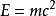公式簡介
其中,E是能量,單位是
焦耳(J)。M是質量,單位是
千克(Kg)。C是真空中
光速(m/s),c=299792458m/s
該公式表明物體相對於一個
參照系靜止時仍然有能量,這是違反牛頓系統的,因為在牛頓系統中,靜止物體是沒有能量的。這就是為什麼物體的質量被稱為靜止質量。公式中的E可以看成是物體總能量,它與物體總質量(該質量包括靜止質量和運動所帶來的質量)成正比,只有當物體靜止時,它才與物體的(靜止)質量(牛頓系統中的'質量')成正比。這也表明物體的總質量和靜止質量不同。
反過來講,一束光子在真空中傳播,其靜止質量是0,但由於它們有運動能量,因此它們也有質量。
表達形式
表達形式1:
上式中的
為物體的靜止質量
,為物體的靜止能量
。中學物理教材中所講的質能方程含義與此表達式相同,通常簡寫為
。
為隨運動速度增大而增大了的質量。
為物體運動時的能量,即物體的靜止能量和動能之和。
上式中的Δm通常為物體靜止質量的變化,即
質量虧損。ΔE為物體靜止能量的變化。實際上這種表達形式是表達形式1的
微分形式.這種表達形式最常用,也是學生最容易產生誤解的表達形式。
術語的不同
注意:有些術語使用中,質量單指靜止質量,因為總質量和能量是等價的概念。若
指代靜止質量,則公式應改寫為而,因此,
也就是
總質量的表達式,其中
為
洛倫茲因子。
推導1
首先要認可
狹義相對論的兩個假設:1、任一光源所發之球狀光在一切
慣性參照系中的速度都各向同性總為c。 2、所有慣性
參考系內的物理定律都是相同的。
如果你的行走速度是v,你在一輛以速度u行駛的公車上,那么當你與車同向走時,你對地面的速度為u+v,反向時為u-v,你在車上過了1分鐘,別人在地上也過了1分鐘——這就是我們腦袋裡的常識。也是物理學中著名的
伽利略變換,整個經典力學的支柱。該理論認為
空間是獨立的,與在其中運動的各種物體無關,而時間是均勻流逝的,線性的,在任何觀察者來看都是相同的。
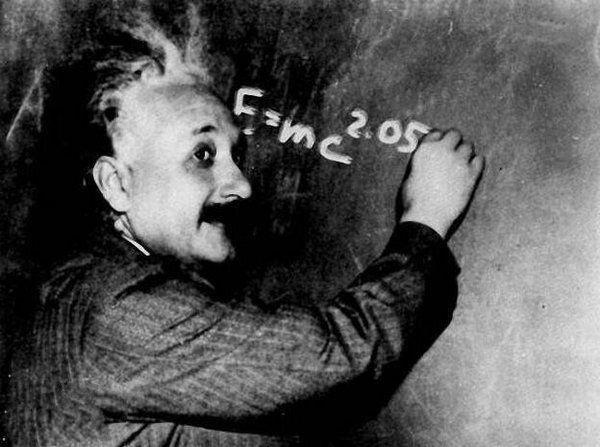 愛因斯坦書寫質能方程
愛因斯坦書寫質能方程而以上這個變換恰恰與狹義相對論的假設相矛盾。
事實上,在
愛因斯坦提出狹義相對論之前,人們就觀察到許多與常識不符的現象。物理學家
洛倫茲為了修正將要傾倒的經典物理學大廈,提出了
洛倫茲變換,但他並不能解釋這種現象為何發生,只是根據當時的觀察事實寫出的
經驗公式——洛倫茲變換——而它卻可以通過相對論的純理論推導出來。
然後根據這個公式又可以推導出質速關係,也就是時間會隨速度增加而變慢,質量變大,長度減小。
一個物體的實際質量為其靜止質量與其通過運動多出來的質量之和。
當外力作用在靜止質量為
的自由
質點上時,質點每經歷
位移,其動能的增量是
,
設外力作用於質點的時間為
,則質點在外力
衝量作用下,其
動量增量是
,
注意到等式右邊為0,即上式可化為
上式說明,當質點的速度v增大時,其質量m和動能Ek都在增加,質量的增量dm和動能的增量
之間始終保持
所示的量值上的正比關係。
上式是相對論中的動能表達式。愛因斯坦在這裡引入了
經典力學中從未有過的獨特見解,他把
叫做物體的靜止能量,把
叫做運動時的能量,我們分別用
和
表示:
,
。
推導:
首先是狹義相對論得到
所以,運動物體的質量
然後利用泰勒展開(展開後第二項為零,此處為第一項和第三項):
得到
其中
為靜止能,
就是我們平時見到的在低速情況下的動能,後面的是高階的能量。
(當可以測出
時,由此公式可以計算出物體運動的絕對速度。)
推導2
根據公式,運動時物體質量增大,同時運動時將會有動能,質量與動能均隨速度增大而增大。
根據,得,因為,所以,由易得。
這就是相對論下的動能公式。當速度為0,,動能為0。為物體靜止時的能量,而 總能量=靜止能量+動能,因此總能量。
影響
這個方程對於
核子彈的發展是關鍵性的。這不僅顯示可能通過輕核的
核聚變和重核的
核裂變釋放這個結合能,也可用於估算會釋放的結合能的量。注意質子和中子的質量還在那裡,它們也代表了一個能量值。
一個著名的花絮是愛因斯坦最初將方程寫為
(用了一個“L",而不是“E"來表示能量,而E在其它地方也用來表示能量)。
重要的是要注意實際的靜質量到能量的轉換不大可能是百分之百有效的。一個理論上完美的轉化是物質和
反物質的湮滅;對於多數情況,有很多帶靜質量的副產品而不是能量,因而只有少量的靜質量真正被轉換。在該方程中,質量就是能量,但是為了簡明起見,轉換這個詞常常被用於代替質能等價關係,實際上通常所指的一般是靜質量和能量的轉換。
相關
靜止能量
物體的靜止能量是它的總內能,包括分子運動的動能、分子間相互作用的
勢能、使
原子與原子結合在一起的化學能、原子內使
原子核和電子結合在一起的
電磁能,以及原子核內
質子、中子的結合能…….物體靜止能量的揭示是相對論最重要的推論之一,它指出,靜止
粒子內部仍然存在著運動。一定質量的粒子具有一定的內部運動能量,反過來,帶有一定內部運動能量的粒子就表現出有一定的慣性質量。在
基本粒子轉化過程中,有可能把粒子內部蘊藏著的全部靜止能量釋放出來,變為可以利用的動能。例如,當π介子衰變為兩個
光子時,由於光子的靜止質量為零而沒有靜止能量,所以π介子內部蘊藏著的是全部靜止能量。
虧損守恆
當一組粒子構成複合物體時,由於各粒子之間有相互作用能以及有相對運動的動能,因而,當物體整體靜止時,它的總能量一般不等於所有粒子的靜止能量之和,即
,其中
為第i個粒子的靜止質量。
與此對應,物體的靜止質量
亦不等於組成它的各粒子的靜止質量之和,兩者之差稱為質量虧損:
由於在
中學物理教材中,對此式的解釋較淺,因此,有些學生就誤認為核反應過程中,質量不再守恆,且少掉的質量轉化為能量了。
守恆定律
在一個孤立系統內,所有粒子的相對論動能與靜能之和在相互作用過程中保持不變,稱為質能守恆定律。
在
相對論里,質能公式
描述了質量與能量存在固定關係。在經典力學中,
質量和能量之間是相互獨立、沒有關係的,但在相對論力學中,能量和質量只不過是物體力學性質的兩個不同方面而已。這樣,在相對論中質量這一概念的外延就被大大地擴展了.愛因斯坦指出:“如果有一物體以輻射形式放出能量ΔE,那么它的質量就要減少
.至於物體所失去的能量是否恰好變成輻射能,在這裡顯然是無關緊要的,於是我們被引到了這樣一個更加普遍的結論上來.物體的質量是它所含能量的量度,”他還指出,“這個結果有著特殊的理論重要性,因為在這個結果中,物體系的慣性質量和能量以同一種東西的姿態出現……我們無論如何也不可能明確地區分體系的‘真實’質量和‘表現’質量。把任何
慣性質量理解為能量的一種儲藏,看來要自然得多。”這樣,原來在
經典力學中彼此獨立的
質量守恆和
能量守恆定律結合起來,成了統一的“
質能守恆定律”,它充分反映了物質和運動的統一性。質能方程說明,質量和能量是不可分割而聯繫著的。一方面,任何物質系統既可用質量m來標誌它的數量,也可用能量E來標誌它的數量;另一方面,一個系統的能量減少時,其質量也相應減少,另一個系統接受而增加了能量時,其質量也相應地增加。

機械能守恆定律的主要公式:
(1 表示物體初狀態,2為末狀態)。
附加項:揭示質能方程的隱藏秘密
能量等於質量及光的平方.實實在在讓人模不著頭腦,能量與質量之比,關光什麼事?
這問題,使絕大部份對研究物理的科學家們頭痛萬分,在公布的最初甚至到現在有些科學家們仍然認為這方程是錯誤的.但無數實驗確確實實的數據顯示,質能方程準確無誤.但其原因,依舊使人迷茫.
對科研人來說,是個''真實而又正確的謎''
1 質能場方程
1.1質能方程的隱藏意義
愛因斯坦的推導,上面公式的實驗結果,這裡就不再貼了,反正很多種推導教科書也有.
這裡我們來看看這方程的隱藏意義.
先來看看光的平方是什麼:
即質能方程可改成:
只是稍微的改變一下這公式的表達式,我們就可看見一個新奇的現象
是真空電容率及真空磁導率,是兩個常用的物理常數,分別表現出電場及磁場在''真空''中的測量點上的值.
這樣,直接以這公式,我們就可以引述一個現象:
質量,是基於
這結構上存在多少E能量而形成的.
所以,質量,是一個由
這結構而來的能量場.
所以
應該寫成下面的表達式:
----我們稱這表達式為''質能場方程''
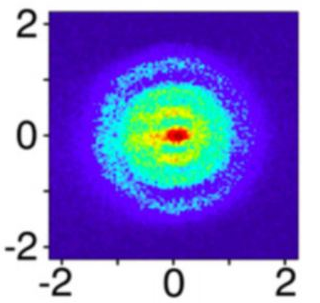
右圖為一個氫元素的雷射拍攝圖
那裡的"光"其實就是雷射在氫元素中因能量場消耗了光的能量而拍攝出來的紅移狀,
所以, 質量, 是一個由空間形成的能量場
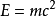
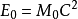
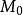
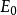
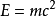
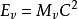

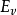
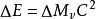
 愛因斯坦書寫質能方程
愛因斯坦書寫質能方程